集合,簡單地說,就是一堆東西的總體,其中每個東西稱為這個集合的一個元素。這樣的集合相念是素朴和直觀的、理解起來并不困難,但它不是嚴格的、精確的。
通過對具體集合的認識,和對集合性質的討論,可以使我們逐步加深對集合這個相念的理解。
例:將甚麼東西也沒有看作一種總體,這樣的集合稱為空集,符號記作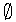 。更多的例子。
。更多的例子。
定義:如果a是A的元素,則稱a屬於A,記作a A。如果a不是A的元素,則稱a不是A的元素,則稱a不屬於A,就作a
A。如果a不是A的元素,則稱a不是A的元素,則稱a不屬於A,就作a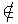 A。
A。
描述集合的兩種方法:
-
用溫氏(Venn)圖用圖在直觀表示集合。
-
列舉法:將集合中的元素一一列舉出來。A={2, 3, 5, 7, ....}
-
描述法來刻劃集合中元素的性質,一般形式可以寫成{ x | P(x) },解作由所有滿足條件P的元素x所組成的集合。條件P可以是複合的。
例自然數集={x | x是整數,x≧0 }。
註:雖然集合論時常當作一切東西的代名詞,但從經驗所知:並不是所有東西都是集合。最簡單的就是羅素(B.Russell)在1918年的理髮師悖論:
“ 小鎮裡僅有一個理髮師,他宣稱專給那些並且只給那些
自己不為自己理髮的人理髮。那麼誰給這位理髮師理髮?”
集合論的悖論例子:
設C是由所有集合所組成的總體。
定義一個(集合)A={ x為C中的元素 | x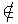 x
}。
x
}。
(不要理會怎樣滿足條件x x
的集合)
x
的集合)
仔細研究以下的兩個問題:
-
A
 A? 答案:不成立。
A? 答案:不成立。
(反證法):如果A A成立,則由A(作為元素來看)滿足定義集合A的條件,即A
A成立,則由A(作為元素來看)滿足定義集合A的條件,即A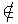 A。這是矛盾。
A。這是矛盾。
-
A
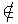 A? 答案:不成立。
A? 答案:不成立。
(反證法):如果A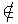 A成立,則由於A不滿足定義的條件,所以A
A成立,則由於A不滿足定義的條件,所以A A成立。但這和假設矛盾。
A成立。但這和假設矛盾。
註:任意兩個集合A、B,由檢查元素後,必定可以知道A=B或A≠B。
以上的悖論,是非常嚴重。因為集合將會是數學的基石,如果這種理論有一些東西有問題,那麼所謂“嚴格的證明”也可能是沒意思。
另外一個例子:考慮以下的正整數:
-
第10,000個素數;
-
數987654321的平方;
-
比π10大的最小整數。
它們有幾個共通點:用不超過一百個印刷符號就可以明確定義。
印刷符號只有有限個。用不超過一百印刷的號能定義的正整數也只有有限個。
下面定義一個正整數A:
“A是用以不超過一百印刷符號不能定義的最小正整數。”
但上面定義的這個正整數 A 恰好是用不超過一百個印刷符號能定義的!
(注意:以上的定義只用了24個符號)
問題在於上面所用的語言中,“能定義”一詞是不精確的。
ZF ( E.Zermelo-A.A.Fraenkel )公理系統是用形式語言來表達的形式系統。所用的形式語言不同於自然語言,是一種人工語言,具有精確、不含混的特點。
ZF系統的語言有以下符號:
-
五個邏輯連接詞:
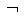 (否定詞)、
(否定詞)、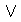 (析取詞)、
(析取詞)、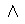 (合取詞)、→(蘊涵詞)、
(合取詞)、→(蘊涵詞)、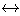 (等價詞);
(等價詞);
-
兩個量詞:
 (全稱量詞)、
(全稱量詞)、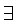 (存在量詞);
(存在量詞);
-
兩個關係詞:=(等詞)、
 (屬詞);
(屬詞);
-
可數個變元:x, y, z, ....(可帶下標);
-
左括號(、右括號)。
以上的符號中若干有限個符號按一定的規則形成的符號串叫作公式,規則有兩條:
-
x
 y、x=y是公式,叫做原子公式,其中x、y可以換成其他變元;
y、x=y是公式,叫做原子公式,其中x、y可以換成其他變元;
-
若φ、ψ是公式,則
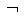 (φ)、(φ)
(φ)、(φ)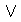 (ψ)、(φ)
(ψ)、(φ)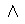 (ψ)、(φ)→(ψ)、(φ)
(ψ)、(φ)→(ψ)、(φ)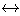 (ψ)、
(ψ)、 x(φ)、
x(φ)、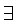 x(φ)都是公式,叫做更詞層之的公式,其中x可換成其他變元。
x(φ)都是公式,叫做更詞層之的公式,其中x可換成其他變元。
形式系統的命題和推理都是用這種語言表達的,對這種形式詞言可作多種解釋。
但的們心目中的解釋是:
| 變元 |
集合; |
|
 |
是...的元素; |
| = |
等於、相等; |
|
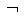 |
否定; |
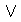 |
(可兼)或; |
|
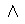 |
與 |
| → |
如果....,那麼... |
|
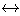 |
當且僅當; |
 x x |
對每個集x...... |
|
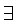 x x |
存在集合x .... |
一個公式就可解釋為某個關於集的命題,或者相反地,把關於集合的命題翻譯成公式。例如
-
公式:
 x( (x
x( (x A)
A)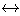 (x
(x B)
) 表示
B)
) 表示
命題:“對於任意集合x,x是A的元素當且僅當x是B的元素”;
-
公式:
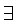 x
x y(
y(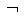 (y
(y x))
表示
x))
表示
命題:“存在著沒有任何成員的集”;
-
命題:“存在把一切集作為自已成員的集”(不論其真假)可翻譯成
公式: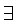 x
x y(y
y(y x)。
x)。
-
命題:“存在著以集A和B為僅有元素的集”可翻譯成
公式: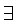 x
x y(
(y
y(
(y x)
x)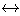 (
(y=A)
(
(y=A)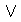 (y=B) )。
(y=B) )。
註:
-
在不引起混淆時,可省去公式中的一些括號。
-
公式
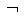 (x=y)、
(x=y)、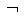 (x
(x y)常被分別寫為x≠y與x
y)常被分別寫為x≠y與x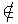 y。
y。
-
為方便,常在公式中引進一些縮寫。例如常把
公式: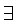 x(x
x(x a
a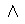 φ(x)
)、
φ(x)
)、 x(x
x(x a→φ(x)
)分別縮寫為
a→φ(x)
)分別縮寫為
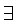 x
x aφ(x)
、
aφ(x)
、 x
x aφ(x)。
aφ(x)。
-
把公式
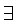 x (φ(x)
x (φ(x)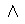
 y(φ(y)→y=x
) )縮寫為
y(φ(y)→y=x
) )縮寫為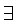 !x φ(x)。
!x φ(x)。
公式的意思是:“唯一存在具有性質φ的x”。
-
有時甚至還在公式中夾進一些普通的語言(必要時可以消去)。
這樣做可做公式的意義更容易理解,不這樣做,公式就會寫的很多,難以閱讀。
-
集合公理,可以用邏輯或集合論中的記號來說明公理的內容。
-
外延公理:
 x
( x
x
( x A
A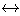 x
x B )
B ) 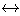 A=B。
A=B。
-
內涵公理:
 S
S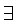 Y
Y x
( x
x
( x Y
Y 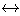 x
x S
S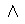 φ(x)
),
φ(x)
),
其中φ(x)是任一不含有變元 y 的公式。
-
無序對公理:
 a
a b
b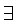 S
( a
S
( a S
S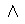 b
b S )。
S )。
-
併集公理:
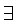 S
S x
x y(
x
y(
x y
y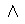 y
y a→
x
a→
x S )。
S )。
對已知集合a,存在著集合s,凡是a的元素的元素都是s的成員。
記s=∪a。時常記A∪B=∪{ A , B } 及A1∪A2∪ ....∪An={A1,
A2, ...., An}。
例:∪{ {a , b}, {c} }={a , b , c}。∪{a}=a。
-
冪集公理:
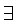 s
s x
( x
x
( x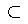 a→ x
a→ x s
)。
s
)。
註:以上的公理只是堂上所講過的集合公理,其實有更多和重要的公理:
-
無限公理:
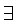 s
( 0
s
( 0 s
s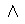
 x
x s
( x∪{x}
s
( x∪{x} s) )。
s) )。
-
替換公理:設集合a和公式φ(x, y)具有性質
 x
x a
a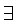 !y
φ(x, y),
!y
φ(x, y),
則 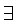 s
s x
x a
a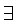 y
y s
φ(x, y)。
s
φ(x, y)。
-
選擇公理:對於任意集合c,存在以c為定義域的選擇函數,使得對於c的每個非空元素x,g(x)
 x。
x。
集合的相等:設A、B為集合,如何判別它們是否相等?這是非常重要的基本概念。
-
集合A、B相等,符號上記為A=B。就是要檢查 x
 A
A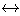 x
x B。
B。
-
由此定義符號
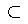 :A
:A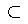 B理解x
B理解x A
→x
A
→x B。
B。
-
A=B 可以理解為A
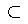 B、B
B、B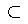 A。
A。
-
其實集合論主要是研究“屬於
 ”的性質。所有的要討論的東西都是“集合”,即使元素也是集合。
”的性質。所有的要討論的東西都是“集合”,即使元素也是集合。
例子:
-
A={ x | x=3a +5b,其中a、b為整數},B={ y | y=7m +10n,其中m、n為整數}。
表面上,A、B的描述方式是不相同,當事實上集合A=B。
證:分兩步討論:
-
A
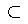 B:設x
B:設x A,則x=3a+5b=7(-a-5b)+10(a+4b)。
A,則x=3a+5b=7(-a-5b)+10(a+4b)。
由於(-a-5b)、10(a+4b)為整數,所以x B。
B。
-
B
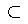 A:設y
A:設y B,則y=7m+10n=3(-m)+5(2m+2n)。
B,則y=7m+10n=3(-m)+5(2m+2n)。
由於-m、(2m+2n)為整數,所以y A。
A。
以上已證明:在(i) x A→x
A→x B;在(ii)中y
B;在(ii)中y B→y
B→y A。
A。
根據外延公理,所以有A=B。
-
試證明:
-
A∩A=A;
-
A∩
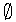 =
=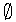 ;
;
-
A∩B=A∩B;
-
若A
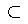 B,則A∩B=A;
B,則A∩B=A;
-
(A∩B)∩C=A∩(B∩C)。
-
試證明:
-
A∪A=A;
-
A∪
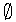 =A;
=A;
-
A∪B=A∪B;
-
若A
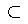 B,則A∪B=B;
B,則A∪B=B;
-
(A∪B)∪C=A∪(B∪C)。
-
試證明:
-
A∩(B∪C)=(A∩B)∪(A∩C),(交對併的分律);
-
A∪(B∩C)=(A∪B)∩(A∪C),(并對交的分配律);
-
A∩(A∪B)=A,(吸收律);
-
A∩(B∪B)=B,(吸收律)。
![]() 。更多的例子。
。更多的例子。
![]() A。如果a不是A的元素,則稱a不是A的元素,則稱a不屬於A,就作a
A。如果a不是A的元素,則稱a不是A的元素,則稱a不屬於A,就作a![]() A。
A。
x }。
x 的集合)
A? 答案:不成立。
A成立,則由A(作為元素來看)滿足定義集合A的條件,即A
A。這是矛盾。
A? 答案:不成立。
A成立,則由於A不滿足定義的條件,所以A
A成立。但這和假設矛盾。